Desigualdades e inecuaciones.
Una desigualdad es una relación de orden que compara dos o más entes matemáticos. Por ejemplo, sean \(\mathbb{R}_1\) y \(\mathbb{R}_2\) dos números reales cualesquiera, sobre ello se puede expresar que \(\mathbb{R}_1=\mathbb{R}_2\) o cualquier otra relación de orden que se desee.
Relaciones de orden menor que y mayor que.
Sean \(\mathbb{R}_1\) y \(\mathbb{R}_2\) dos números reales tales que \(\mathbb{R}_1\neq\mathbb{R}_2\) entonces dichos números pueden compararse mediante la relación de orden menor que o mayor que como sigue:
Definición de la relación menor que: para dos números reales cualesquiera \(\mathbb{R}_1\) y \(\mathbb{R}_2\) se dice que \(\mathbb{R}_1\) es menor que \(\mathbb{R}_2,\) lo cual se escribe \(\mathbb{R}_1<\mathbb{R}_2\) si y solo si la diferencia \(\mathbb{R}_2-\ \mathbb{R}_1\) es positiva, lo cual se escribe como \(\mathbb{R}_1<\mathbb{R}_2 \Longleftrightarrow \mathbb{R}_2-\ \mathbb{R}_1=\mathbb{R}^+\)
Definición de la relación mayor que: para dos reales cualesquiera \(\mathbb{R}_1\) y \(\mathbb{R}_2\) se dice que \(\mathbb{R}_1\) es mayor que \(\mathbb{R}_2,\) escrito como \(\mathbb{R}_1>\mathbb{R}_2,\) si y solo si, la diferencia \(\mathbb{R}_2-\mathbb{R}_1\) es negativa, lo cual se escribe como \(\mathbb{R}_1>\mathbb{R}_2 \Longleftrightarrow \mathbb{R}_2-\mathbb{R}_1=\mathbb{R}^-.\)
Gráficamente en la recta real se tiene que, para los reales \(\mathbb{R}_1\) y \(\mathbb{R}_2\) es mayor, el que está ubicado a la derecha del otro. De manera equivalente decir, que \(\mathbb{R}_1<\mathbb{R}_2\) implica que \(\mathbb{R}_2>\mathbb{R}_1.\) En la gráfica de más abajo \(\mathbb{R}_1<\mathbb{R}_2.\)

Una inecuación es una desigualdad la cual involucra una o más incógnitas, por ejemplo, si en la desigualdad \(5< 13\) se escribe \(5x< 13\) o \(5< 13x\) la desigualdad ahora es llamada una inecuación. De modo que “todas las inecuaciones son desigualdades, pero no todas las desigualdades son inecuaciones”
Una desigualdad puede ser estricta o no. Una desigualdad estricta es aquella en la cual \(a< n\) o \(a>n\), mientras que una desigualdad no estricta (también llamadas amplias por algunos autores) es una desigualdad en la cual \(a\le n\) o \(a\geq n\).
Resolver una inecuación es determinar el conjunto de todos los valores que hacen la desigualdad verdadera, el cual es llamado conjunto solución. La representación gráfica de este conjunto en la recta real, recibe el nombre de gráfica de la desigualdad.
Al resolver una desigualdad el axioma de las ecuaciones se cumple de manera parcial, de modo que no siempre realizar la misma operación en ambos miembros produce una inecuación equivalente, este hecho se resume como sigue.
Axioma de las ecuaciones aplicado a las desigualdades.
Sean \(a,\ m\) y \(n\) tres números reales cualquieras donde \(a\neq0\) entonces se tiene:
1. Sumar o restar una misma cantidad en ambos miembros no altera la desigualdad.
Si \(n< m\) entonces \(n\pm a< m\pm a.\)
2. Multiplicar ambos miembros por un número positivo no altera la desigualdad. Si \(a>0\) y \(n< m\) entonces \(an< am\).
3. Multiplicar (o dividir) una desigualdad por un número negativo cambia el sentido de la desigualdad.
Si \(a< 0\) y \(n< m\) entonces \(an>am.\)
4. Las afirmaciones anteriores son válidas también para \(n>m n\le m, n\geq m.\)
Inecuaciones lineales.
Se dice que una inecuación lineal es una desigualdad de grado uno.
A diferencia de las ecuaciones lineales, cuando se resuelve una inecuación lineal no se obtiene un único valor sino, un conjunto de valores que satisfacen la inecuación, llamado conjunto solución.
Ejemplo 1. Resolución de inecuaciones lineales. Resolver las inecuaciones siguientes: \(a.~3x+5<-12~~\) y \(~~b.~-8x+3>13\)
$$\begin{array}{c |c} \mathrm{Solución}~ 1: & \mathrm{Solución}~ 2:\\ 3x+5<-12 & -8x > 13-3\ \ \mathrm{Trasposición.}\\ 3x<-12-5\ \ \ \mathrm{Trasposición} & -8x > 10\ \ \ \ ~~~~~~ \mathrm{Simplificando}\\ 3x<-17\ \ \ \ ~~~~~~ \mathrm{Simplificación}& x<\frac{10}{-8}\ \ \ \ ~~~~~~~~~ \mathrm{Despejando}\\ x<-\frac{17}{3}\ \ \ \ ~~~~~~~ \mathrm{Despejando}~ x.& x<-\frac{5}{4}\ \ \ \ \ ~~~~~~~\mathrm{Despejando} \end{array}$$

Note que ambas graficas tienen un hueco (punto en blanco o vacío) esto es porque las desigualdades son estrictas.
Ejemplo 2. Resolver la desigualdad
$$\frac{5}{3}x-\frac{4}{5}\le\frac{7}{2}x+3$$
Solución: multiplique por el m.c.ds. para convertir las fracciones a números enteros y luego aplique propiedades de inecuaciones.
\begin{align}
&30\left(\frac{5}{3}x-\frac{4}{5}\right)\le 30\left(\frac{7}{2}x+3\right)\\
&50x-24\le105x+90\\
&50x-105x\le90+24\\
&-55x\le114\\
&x\geq-\frac{114}{55}\end{align}
Recuerde que dividir una desigualdad entre un número negativo cambia el sentido de la desigualdad.
La solución gráfica se muestra en color rosa.
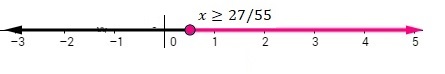
Notación de intervalo y concepto de infinito.
Al trabajar con inecuaciones muchas veces es necesario escribir de una manera más simple el conjunto numérico que expresa la solución, una forma alternativa es mediante el uso de intervalos. Sean \(a\) y \(b\) dos números reales cualesquiera, entonces se dice que un intervalo \(a\) coma \(b\) es el conjunto de todos los números reales comprendido entre \(a\) y \(b\) . Los números \(a\) y \(b\) son llamados extremos del intervalo y pueden pertenecer o no al él.
Según se incluya o no los valores extremos del intervalo estos se clasifican en:
\(1.\) Intervalo abierto \(\left(a,b\right)\) no incluye los puntos extremos \(a\) y \(b\).
\(2.\) Intervalo cerrado \(\left[a,b\right]\) incluye los puntos extremos \(a\) y \(b\).
\(3.\) Intervalo semiabierto por la izquierda \(\left(a,b\right]\) no incluye el punto extremo \(a\).
\(4.\) Intervalo semiabierto por la derecha \(\left[a,b\right)\) no incluye el punto extremo \(b\).
Concepto de infinito.
En ocasiones se expresan desigualdades las cuales no tienen un límite establecido. ¿Qué significado tiene decir “la cantidad mínima es \(1kg\)” "el peso máximo es \(200N\)" o “\(x\) es mayor que siete” ¿Se pueden escribir todos los valores posibles para las desigualdades?
Para tales casos las matemáticas se valen del concepto de infinito representado por una lemniscata \(\infty.\)
Al decir que una cantidad \(x\) crece o decrece sin límites, o que puede tomar infinitos valores se expresa “\(x\) tiende a infinito” lo cual se escribe \(x\rightarrow\infty,\) (o menos infinitos \(-\infty\)), pero tenga en cuenta que infinito no es número, por tanto, carece de sentido pensar que \(\infty+\infty=2\infty\) o \(\infty-\infty=0\) tales afirmaciones son falsas.
Si un número \(x\) pertenece a un intervalo cualquiera \(a\) coma \(b,\) se escribe en forma de una desigualdad simultánea (que sucede a la vez) \(a < x< b\) (para un intervalo abierto). Así al indicar que un número \(x\) es mayor que cinco y menor que siete se escribe \(5 < x < 7,\) es decir \(x\) pertenece al intervalo \(\left(5,\ 7\right).\) Si en cambio se expresa que \(x\) es mayor o igual que cinco y menor que siete, entonces se escribe \(5\le x< 7\) (notación de desigualdad) que en notación de intervalo es \(\left[5,\ 7\right).\)
A partir de los conceptos de infinito e inecuaciones simultaneas se pueden escribir intervalos abierto y semi abiertos mediante el uso de la notación de desigualdades finitas o infinitas como se muestra en la tabla siguiente.

Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Inecuaciones no lineales
Se dice que una desigualdad o inecuación es no lineal si posee algún exponente no lineal, o está expresada como el cociente de dos polinomio.
Ejemplos de desigualdades no lineales son las expresiones, $$\mathbf{1}.\ \ 2x^2+x\geq1\ \ \ \ \ \ \ \ \mathbf{2}.\ \ 2x^3-3x^2\le11x-6$$$$\mathbf{3}.\ \ \ \frac{3x-5}{2x+3}\le6\ \ \ \ \ \ \ \mathbf{4}.\ \ \frac{5}{2x+3}>\frac{2}{3x+1}~~~$$ donde uno y dos son desigualdades polinómicas de segundo y tercer grado respetivamente, mientras que tres y cuatro son desigualdades racionales (cociente de polinomios).
Resolución de inecuaciones no lineales.
Al igual que en las inecuaciones lineales, resolver una inecuación no lineal es determinar lo valores que hacen la desigualdad verdadera.
Para determinar el conjunto solución de una inecuación no lineal se debe,
1. Escribir la inecuación en forma general (ordenada descendente y segundo miembro igual cero).
2. Factorizar el primer miembro, igualando a cero cada factor, para determinar así los intervalos sobre la recta real.
3. Evaluar cada factor dentro de cada intervalo (para ello se toma un valor de prueba) y basados en las premisas de los signos de una expresión algebraica realizar la conclusión.
Ejemplo. Determinar los valores para los cuales \(2x^2+x\geq1\).
Comience por escribir la inecuación como \(2x^2+x-1\geq0,\) luego factorice y determine los puntos críticos (p.c.) de la desigualdad \(\left(x+1\right)\left(2x-1\right)\geq0\) por tanto \(x=-1\) y \(x=1/2\) son p.c.
$$\begin{array}1
\mathrm{Intervalo}& (-\infty,-1) & (-1,1/2) & (1/2,\infty)\\
\hline \mathrm{signo ~de}~x+1&-&+&+\\
\hline \mathrm{signo~de}~2x-1&-&-&+\\
\hline (x+1)(2x-1)& +& -&+\\
\hline
\end{array}$$
De donde \((x+1)(2x-1)\geq0\) para el primer y tercer intervalo, por tanto, el conjunto solución es\((-\infty,-1]∪[12,∞)\).
Ejemplo. Determinar los valores para los cuales \(2x^3-3x^2\le 11x-6\)
Comience por escribir la inecuación con el miembro de l derecha igualado a cero en la forma \(2x^3-3x^2-11x+6\le0\).
Factorice y determine los ceros del polinomio del miembro de la izquierda, esto es,
\((x+2)(2x-1)(x-3)=0\) por tanto, los ceros del polinomio son \((x_1=-2,~~x_2=1/2,~~x_3=3\).
Verifique ahora mediante una tabla la condición de la igualdad.
$$\begin{array}1
\hline \mathrm{Intervalo}& (-\infty,-2)& (-2,1/2)& (1/3,3) & (3,\infty)\\ \hline
\mathrm{signo~de}~ x+2& -& +& +& +&\\ \hline
\mathrm{signo~de}~ 2x-1& -& -& +& +&\\ \hline
\mathrm{signo~de}~ x-3& -& - &- &+&\\ \hline
(x+2)(2x-1)(x-3)& -& +& -& +&\\
\hline\end{array}$$
Luego el conjunto solución es \((-\infty,-2]∪[12,3]\).
Ejemplo. Determinar los valores para los cuales $$\frac{x-5}{2x+3}\le6$$
Solución: comience por escribir el segundo miembro de la expresión igual a cero.
\begin{align}
&\frac{3x-5}{2x+3}-\frac{6}{1}\le0\\
&\frac{1(3x-5)-6(2x+3)}{2x+3}\le0\\
&\frac{3x-5-12x-18}{2x+3}\le0\\
&\frac{-9x-23}{2x+3}\le0\\
&-\frac{9x+23}{2x+3}\le0\\
&\frac{9x+23}{2x+3}\geq0\end{align}
Construyendo ahora una tabla para verificar la desigualdad se tiene,
$$\begin{array}1
\mathrm{Intervalo} &(-\infty,-23/9) &(-23/9,-3/2)& (-3/2,\infty)\\ \hline
\mathrm{signo~ de~} 9x+23 &- &+ &+\\ \hline
\mathrm{signo~ de~} 2x+3 & -& -& +&\\ \hline
\frac{9x+23}{2x+3}& +& -& +&\\ \hline
\end{array}$$
Luego el conjunto solución es,
\((-\infty,\ -23/9]∪[-3/2,\infty)\)
Ejemplo. Determinar los valores para los culaes $$\frac{5}{2x+3}>\frac{2}{3x+1}$$ Solución: se debe tener cuidado de proceder igual que en las ecuaciones y multiplicar por el \(m.c.ds.\) de los denominadores, esto no es correcto ya que al hacerlo no se sabe si se está multiplicando por un número negativo o positivo, así que no se sabe si la desigualdad debe o no cambiar de sentido. Lo correcto es convertir un miembro en cero y proceder con las operaciones en el otro, como sigue. $$\frac{5}{2x+3}-\frac{2}{3x+1}>0$$ $$\frac{5(3x+1)-2(2x+3)}{(2x+3)(3x+1)}>0$$ de donde se tiene: $$\frac{11x-1}{(2x+3)(3x+1)}>0$$ Construyendo ahora una tabla para comprobar la desigualdad. $$\begin{array}1 \mathrm{Intervalo} &\left(-\infty,-\frac32\right)& \left(-\frac32,-\frac13\right)&\left(-\frac13,\frac1{11}\right) &\left(\frac1{11},\infty\right)\\ \hline \mathrm{signo~de~} 11x-1 &-& -& - &+\\ \hline \mathrm{signo~de~} 2x+3 & -& +& +& +\\ \hline \mathrm{signo~de~} 3x+1& -& -& +& +\\ \hline (2x+3)(3x+1)& +& -& +& +\\ \hline \frac{11x-1}{(2x+3)(3x+1)}& -& +& -& +\\ \hline \end{array}$$ Tomando el cociente de los signos de las filas uno y cuatro, se concluye que el conjunto solución está formado por los intervalos \((-3/2,-1/3) \cup(1/11,\infty)\).
